蒙特卡洛积分(Monte Carlo Integration)是一种基于随机数和概率统计原理的数值积分方法。与传统的确定性积分方法(如梯形法、辛普森法等)不同,蒙特卡洛积分特别适用于高维积分和复杂区域的积分计算。以下是对蒙特卡洛积分的详细介绍:
基本原理
蒙特卡洛积分的核心思想是通过在积分区域内随机采样点,利用这些点的函数值来估算积分的结果。具体步骤如下:
-
确定积分区域和被积函数:设需要计算的积分为
![Rendered by QuickLaTeX.com \[I=int_{0}^{} f(x)dx\]](https://zhangkangblog.com/wp-content/ql-cache/quicklatex.com-9a832d3b937592031e9dde2e23481edc_l3.png)
At first, we sample
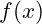 in the
in the 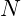 (
(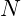 is odd) equidistant points around
is odd) equidistant points around 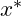 :
:![Rendered by QuickLaTeX.com \[ f_k = f(x_k),\: x_k = x^*+kh,\: k=-\frac{N-1}{2},\dots,\frac{N-1}{2} \]](https://zhangkangblog.com/wp-content/ql-cache/quicklatex.com-8c6733b56a6b126c9ec95813c05a70c1_l3.png)
where
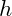 is some step.
is some step.
Then we interpolate points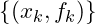 by polynomial
by polynomial
(1)
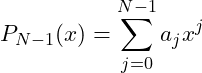
Its coefficients
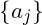 are found as a solution of system of linear equations:
are found as a solution of system of linear equations:
(2)
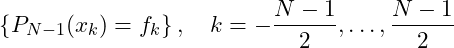
Here are references to existing equations: (1), (2).
Here is reference to non-existing equation (??).
其中 D 是积分区域,f(x) 是被积函数。
生成随机点:在积分区域 D 内生成大量均匀分布的随机点。
计算函数值:计算每个随机点的函数值f(xi)。
估算积分值:积分的估计值为这些函数值的平均值乘以区域 D 的体积 V:
数学表达
假设 N 个随机点均匀分布在区域 D 内,则蒙特卡洛积分的估计值为:
其中:
-
V 是积分区域 D 的体积(在一维情况下为区间长度)。
-
N 是采样点的数量。
-
f(xi) 是函数在第 i 个采样点的值。
特点与应用
-
高维积分:蒙特卡洛积分在处理高维积分时效果显著,因为其计算复杂度与维数的增长关系较弱,适用于维数较高的积分问题。
-
复杂区域:对于形状复杂或不规则的积分区域,蒙特卡洛积分提供了一种简单有效的计算方法,无需对区域进行复杂的分割或变换。
-
计算机模拟:广泛应用于物理学(如粒子模拟)、金融学(如期权定价)、统计学(如贝叶斯推断)等领域,特别是在需要进行大量随机模拟的场景中。
优点
-
易于实现:蒙特卡洛积分的算法相对简单,容易在计算机上实现。
-
适应性强:适用于高维和复杂区域的积分问题,传统方法往往难以处理。
-
并行计算:由于各个采样点的计算相互独立,蒙特卡洛积分非常适合并行计算,能够充分利用现代多核处理器和分布式计算资源。
缺点
收敛速度较慢:蒙特卡洛积分的误差通常以
![]()
的速率收敛,这意味着为了提高精度,需要大量的采样点,计算成本较高。
随机性带来的不确定性:结果具有随机波动性,需要通过增加样本量或采用其他方差减小技术(如重要性采样、控制变量法等)来提高估计的准确性。
示例
假设需要计算二维区域 D 上的积分:
![]()
![]()
使用蒙特卡洛积分的方法,可以按照以下步骤进行:
-
在 [0,1]×[0,1] 区域内生成 N 个随机点
![Rendered by QuickLaTeX.com \[(x_i, y_i)\]](https://zhangkangblog.com/wp-content/ql-cache/quicklatex.com-bbd65e9ece5e6ad49086640c5b7a137d_l3.png)
-
计算每个点的函数值
![Rendered by QuickLaTeX.com \[f(xi,yi)\]](https://zhangkangblog.com/wp-content/ql-cache/quicklatex.com-ff1e23b6a48f3e55b99c4e2a4a9efee5_l3.png)
-
估算积分值为:
![Rendered by QuickLaTeX.com \[I approx frac{1}{N} sum_{i=1}^{N} f(x_i, y_i)\]](https://zhangkangblog.com/wp-content/ql-cache/quicklatex.com-85c3e15c970465994fa57122705f158c_l3.png)
通过增加 N,可以逐步提高估计的精度。
总结
蒙特卡洛积分是一种强大的数值积分工具,尤其在处理高维和复杂区域的积分问题时表现出色。尽管其收敛速度较慢,但随着计算能力的提升和并行计算技术的发展,蒙特卡洛积分在许多科学和工程领域中得到了广泛应用。结合其他优化技术,蒙特卡洛积分的效率和准确性可以进一步提升,使其在实际应用中更加实用。
蒙特卡洛积分所属学科:
蒙特卡洛积分(Monte Carlo Integration)是一种跨学科的方法,涉及多个领域的知识和技术。具体来说,它主要属于以下几个领域:
1. 数学
蒙特卡洛积分源自数学,特别是数值分析和概率论。在数值分析中,蒙特卡洛方法被用来近似计算积分、求解微分方程等问题。其核心思想依赖于概率和统计原理,通过随机采样来估计积分的值。
2. 统计学
统计学在蒙特卡洛积分中扮演重要角色。该方法依赖于随机变量和概率分布,通过大量随机样本的统计特性来估计积分值。统计学中的方差分析和置信区间等概念也常用于评估蒙特卡洛积分的精度和可靠性。
3. 计算机科学与算法
蒙特卡洛积分在计算机科学中被视为一种算法,特别是在数值计算和高性能计算领域。它需要高效的随机数生成器和并行计算技术,以处理大量的随机样本和复杂的计算任务。随着计算机硬件的发展,蒙特卡洛方法得以在大规模和高维问题中广泛应用。
4. 应用科学与工程
蒙特卡洛积分广泛应用于物理学、金融工程、工程学、生物信息学等多个应用领域。例如:
-
物理学:用于粒子模拟、量子力学计算等。
-
金融工程:用于期权定价、风险评估等。
-
工程学:用于可靠性分析、优化设计等。
-
生物信息学:用于基因序列分析、蛋白质折叠预测等。
5. 交叉学科
蒙特卡洛积分作为一种通用的数值方法,常常出现在多个学科的交叉领域。例如,在机器学习中,蒙特卡洛方法用于贝叶斯推断和深度学习模型的训练。在环境科学中,用于模拟气候变化和生态系统动态。
蒙特卡洛积分并不局限于单一的学科领域,而是融合了数学、统计学、计算机科学及多个应用科学的知识与技术。它作为一种强大的数值方法,在理论研究和实际应用中都具有重要地位。通过结合不同领域的优势,蒙特卡洛积分能够高效地解决复杂的积分问题,特别是在高维和复杂区域的情境下表现出色。
如果你对蒙特卡洛积分的具体应用或其在某一特定领域中的角色有进一步的疑问,欢迎继续提问!
积分:
积分是什么
积分(Integration)是微积分学的两个基本概念之一(另一个是导数),用于描述和计算量的累积。积分在数学、物理、工程以及计算机科学等多个领域中具有广泛的应用。根据积分的不同性质,主要分为不定积分和定积分两种。
1. 不定积分
不定积分,也称为原函数,是指找到一个函数F(x),使得其导数等于被积函数 f(x):
![]()
2. 定积分
-
定积分用于计算函数在某一区间内的累积量,如面积、体积等。对于连续函数 f(x)f(x)f(x) 在区间 [a,b] 上的定积分定义为:
![Rendered by QuickLaTeX.com \[∫ a b f(x)dx\]](https://zhangkangblog.com/wp-content/ql-cache/quicklatex.com-2f4f04e62dd493044881652bf64cf53d_l3.png)
几何上,定积分可以表示为曲线 y=f(x)y = f(x)y=f(x) 与 xxx-轴之间在区间 [a,b] 内的面积。
积分的基本性质
-
线性性质:积分具有线性性质,即 ∫(af(x)+bg(x))dx=a∫f(x)dx+b∫g(x)dxint left( a f(x) + b g(x) right) dx = a int f(x) dx + b int g(x) dx∫(af(x)+bg(x))dx=a∫f(x)dx+b∫g(x)dx
-
换元法:通过变量替换简化积分计算。
-
分部积分法:用于处理两个函数的乘积的积分。
-
积分在计算机图形学中的应用
计算机图形学是研究如何在计算机中生成和处理图像的学科,积分在其中扮演着至关重要的角色,涉及多个方面的应用。以下是积分在计算机图形学中的主要应用领域:
1. 渲染(Rendering)
渲染是将三维模型转换为二维图像的过程,积分在光线追踪(Ray Tracing)和全局光照(Global Illumination)中尤为重要。
-
光线追踪:计算光线与场景中物体的交互,需要积分来求解光的传播和反射。
-
全局光照:包括间接光照的计算,涉及复杂的积分来模拟光在场景中的多次反射和散射。例如,辐射度方法(Radiosity)使用积分来计算表面之间的能量传递。
2. 纹理映射与采样
在纹理映射过程中,需要对纹理进行采样和过滤,积分用于计算像素颜色的平均值或加权值,以实现抗锯齿和纹理平滑。
-
抗锯齿:通过积分计算像素区域内的颜色平均值,减少锯齿效应。
-
MIP Mapping:使用积分计算不同分辨率纹理的预过滤版本,优化渲染质量和性能。
3. 几何处理
积分用于几何形状的处理和分析,包括曲面的参数化、体积计算和碰撞检测等。
-
曲面参数化:将三维曲面展开到二维平面,涉及积分计算以保持曲面的性质。
-
体积计算:计算复杂几何体的体积和表面积,需要多重积分。
4. 动画与物理模拟
在动画和物理模拟中,积分用于描述物体的运动、力的作用和能量的变化。
-
动力学模拟:通过积分求解物体的加速度、速度和位移。
-
流体动力学:模拟流体运动需要积分计算流体的速度场和压力场。
5. 光照与阴影
积分用于计算场景中的光照分布和阴影效果,尤其是在软阴影和体积光照中。
-
软阴影:通过积分计算多个光源样本的阴影效果,实现柔和的边缘。
-
体积光照:模拟光在大气中的散射,需要积分计算光的传播路径和散射强度。
6. 图像处理
在图像处理和计算机视觉中,积分用于滤波、边缘检测和特征提取等任务。
-
卷积操作:许多图像滤波器本质上是对图像进行积分(卷积),如模糊、锐化和边缘检测滤波器。
-
边缘检测:使用积分计算梯度或其他边缘特征,识别图像中的边缘。
7. Monte Carlo 方法
蒙特卡洛积分是一种随机采样方法,用于高维积分和复杂场景的渲染。
-
路径追踪(Path Tracing):一种基于蒙特卡洛方法的渲染技术,通过随机采样光线路径来逼近真实光照。
-
全局光照计算:利用蒙特卡洛积分估算复杂的光照方程,处理多次反射和折射。
总结
积分作为数学中的基本工具,在计算机图形学中有着广泛且深远的应用。从光照计算、渲染技术到几何处理和图像处理,积分帮助图形学算法实现更高的逼真度和复杂性。随着计算能力的提升和算法的发展,积分在计算机图形学中的应用将继续扩展,为生成更加真实和复杂的图像提供支持。
如果你对积分在计算机图形学中的某一具体应用有更深入的兴趣或疑问,欢迎进一步提问!
加权平均:
实现积分的编码方法在某些情况下确实涉及到对函数值进行加权平均,但这只是数值积分方法中的一种基本思想。不同的数值积分技术采用不同的加权策略,以更准确地逼近积分值。
数值积分与加权平均
数值积分(Numerical Integration)是通过离散化的方法近似计算定积分的值。其核心思想通常涉及对被积函数在积分区间内的多个点进行采样,并根据这些采样点的函数值计算加权和或平均值。这些加权策略的设计旨在提高积分的精度和效率。
常见的数值积分方法
1. 矩形法(Riemann Sums)
-
描述:将积分区间分割成若干小区间,用矩形的面积近似曲线下的面积。
-
实现:在每个小区间内选择一个采样点(如左端点、右端点或中点),计算函数值并乘以小区间的宽度,再将所有矩形面积相加。
-
与加权平均的关系:实际上,这是一种未加权或均匀加权的平均,因为每个采样点的权重相同,即小区间的宽度。
2. 梯形法(Trapezoidal Rule)
-
描述:用梯形的面积来近似积分区域的面积,考虑到函数值的变化。
-
实现:对于每个小区间,计算两个端点的函数值的平均值,再乘以小区间的宽度。
-
与加权平均的关系:这是对两个端点函数值的简单加权平均(权重均为0.5)的应用。
3. 辛普森法(Simpson’s Rule)
-
描述:利用二次多项式(抛物线)来近似函数,并计算其下的面积。
-
实现:每两个小区间为一组,使用三个采样点(两个端点和一个中点)计算加权和,权重分别为1、4、1,然后将结果乘以区间宽度的六分之一。
-
与加权平均的关系:这里采用了不同的权重(1, 4, 1),从而提高了积分的精度。
4. 高斯求积(Gaussian Quadrature)
-
描述:通过选择最佳的采样点和权重来最大化多项式的积分精度。
-
实现:计算特定节点(采样点)上的函数值,并将其乘以对应的权重,再求和。
-
与加权平均的关系:这是一种更复杂的加权平均方法,权重和节点是通过数学优化确定的,以提高积分的准确性。
5. 蒙特卡洛积分(Monte Carlo Integration)
-
描述:利用随机采样的方法,特别适用于高维积分和复杂区域。
-
实现:在积分区域内随机生成大量点,计算这些点的函数值的平均值,再乘以区域的体积。
-
与加权平均的关系:这是典型的加权平均应用,函数值的平均代表了积分的估计值。由于点是随机生成的,理论上所有点的权重相同,但实际应用中可以结合重要性采样等技术调整权重以减少方差。
积分编码实现中的加权策略
虽然许多数值积分方法涉及对函数值进行某种形式的加权平均,但具体的加权策略因方法而异:
-
简单平均:如蒙特卡洛积分中的基本方法,所有采样点的权重相同。
-
加权平均:如梯形法、辛普森法和高斯求积,采用不同的权重分配,以提高精度。
-
自适应加权:在某些高级方法中,权重可能根据函数的变化自动调整,以更好地捕捉函数的特性。
计算机图形学中的积分实现
在计算机图形学中,积分的实现尤为重要,特别是在渲染(Rendering)和光照计算(Lighting Calculation)中。以下是积分在计算机图形学中的具体应用及其实现方式:
1. 光线追踪(Ray Tracing)和路径追踪(Path Tracing)
-
描述:模拟光线在场景中的传播和与物体的交互,以生成逼真的图像。
-
积分实现:需要对光源的所有可能路径进行积分,计算每条路径对最终像素颜色的贡献。
-
实现方式:通常采用蒙特卡洛积分,通过随机采样多个光线路径,计算其贡献的平均值以估计积分值。
2. 全局光照(Global Illumination)
-
描述:考虑光线的多次反射和散射,模拟间接光照效果。
-
积分实现:涉及对场景中所有可能的光传输路径进行积分。
-
实现方式:使用蒙特卡洛方法或其他数值积分技术,通过大量采样估计间接光照。
3. 纹理映射与抗锯齿
-
描述:将高分辨率纹理映射到三维模型表面,同时减少锯齿现象。
-
积分实现:计算像素区域内的平均颜色或采样值,以平滑图像。
-
实现方式:使用加权平均(如梯形法或简单平均)对多个纹理样本进行积分,获得抗锯齿效果。
4. 物理模拟
-
描述:模拟物体的运动、流体动力学、光照等物理现象。
-
积分实现:通过对物理量(如速度、加速度、能量)的变化进行积分,预测物体状态。
-
实现方式:采用数值积分方法(如欧拉法、龙格-库塔法)来解决微分方程,模拟物理过程。
总结
虽然数值积分的实现通常涉及对函数值进行加权平均,但这只是一个简化的描述。实际的数值积分方法通过精心设计的权重和采样策略,以提高积分的准确性和效率。特别是在计算机图形学中,积分方法不仅用于简单的加权平均,还涉及复杂的采样和优化技术,以实现高质量的图像渲染和物理模拟。



